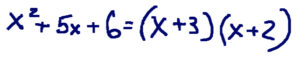
You will encounter at least one factoring problem on SAT Math test. This post walks you through how to factor a quadratic equation from an expanded form into the factored form.
The expression in the expanded form looks like this
X2 + bX + c = 0
But the same expression with factors looks like this
(X + d)(X+e) = 0
where b, c, d and e are numeric constants, like 3, 5, -8 or any other real number.
In order to change the quadratic equation from the expanded form into factored, first, let’s represent b and c in terms of d and e:
b= d + e and c = d * e
Now let’s substitute b and c with d and e in the original equation X2+ bX + c = 0.
So we have
X2 + (d + e)X + de = 0 or
X2 + dX + eX + de = 0
What common factors can we factor out of the first two addition terms? Looks like X repeats itself in both terms, so let’s factor out X from the first two terms.
X(X+d) + eX + de = 0
What common factors can we factor out of the last two addition terms? Looks like e repeats itself in both terms, so let’s factor out e from the last two terms.
X(X+d) + e(X+d) = 0
Now we have two addition terms X(X+d) and e(X+d).
We can clearly see that (X+d) repeats itself in both terms.
So let’s factor out (X+d) from these two terms, so we have
(X+d)(X+e) = 0
This is the form that we need, so we end off here.
Example
We have an equation
X2 + 5x + 6 = 0
We know that the above equation is in the form
X2 + bX + c = 0
and that we need to change it into the form
(X+d)(X+e) = 0,
where b= d + e and c = d * e
So let’s substitute:
Since b=5, then 5=d+e and
since c=6, then 6=d*e
Now we need to find factors d and e for 6 that would also satisfy the equation 5=d+e and 6=d*e.
Let’s list all the possible factors of 6: 1, 6, 2, 3, -1, -6, -2, -3.
Now try to plug the factors into the above two equations 5=d+e and 6=d*e.
If we use the first set of factors, 1 and 6, they would satisfy the equation of
6 = d*e or 6 = 1*6
But would 1 and 6 satisfy the equation 5=d+e?
Let’s try, 6+1 = 7, but we need the sum to be 5, so this combination wouldn’t work.
Let’s move onto the other factors.
We’ll try factors 2 and 3.
Do they satisfy the equation 6 = d*e?
Yes, they do, since 2 * 3 = 6.
We need to see if they satisfy the other equation of d+e=5.
They do satisfy this equation as well, 2+3 = 5.
Since these two factors, 2 and 3 satisfy both equations, they are the factors we’re going to use in the equation.
So let’s factor X2+5x+6 = 0 using factors 2 and 3
We’ll substitute 3+2 instead of number 5 and 3*2 instead of number 6.
X2 + (3+2)x + 3*2 = 0
Now we’ll open the parenthesis and we get
X2+3X+2X+3*2 = 0
What is the common variable or constant for the first two terms for this sum?
It looks like it’s X, so let’s factor X out of the first two terms, so we have
X(X+3)+2x+3*2= 0
What can we factor out of the last two terms of this sum?
It looks like the common factor is 2 for the last two terms of the sum.
So let’s factor 2 out of the last two terms
X(X+3)+2(x+3)= 0
Now we have two addition terms, X(X+3) and 2(X+3).
They have one common factor (X+3), so let’s factor it out, so we get
(X+3)(X+2)=0
And this is our answer.
Practice Problems
Now you should continue practicing factoring quadratics. Work on factoring these expressions and feel free to sign up for a session if you’re running into trouble solving these. I offer both online and in-person sessions.
X2 + 2x – 3 = 0
X2 – 6x + 8 = 0
X2 + 10x + 16 = 0
SAT Math Example Problem
2X(2X+3) + 4(2X+3) = aX2 + bX + c
In the equation above, a, b and c are constants. If the equation is true for all values of X, what is the value of b?
We need to change the left side of the equation into the expanded form, that would take the form of the equation on the right. When we do that, we’ll be able to identify coefficients a, b and c for this equation.
The left side of the equation has two addition terms 2X(2X+3) and 4(2X+3).
Both terms have one factor in common, which is (2X+3).
Let’s factor out (2X+3)
(2X+3) (2X+4) = aX2 + bX + c
Now we’re going to use distributive property of addition over multiplication. Each term inside the first parentheses needs to be multiplied by each term inside of the second parenthesis.
2X*2X + 2X*4 + 3*2X + 3*4 = aX2 + bX + c
Now let’s multiply
4X2 + 8X + 6X + 12 = aX2 + bX + c
Now let’s add the like terms on the left side
4X2 + 14X + 12 = aX2 + bX + c
Now our equation on the left side is in the same form as the equation on the right side. We can see that a=4, b=14 and c=12.
The question was, what is the value of b? The answer is 14.
SAT Math Practice
Try this one on your own
Y = X2 – 8X + 15
The equation above represents a parabola in the XY-plane. Which of the following equivalent forms of the equation displays the X-intercepts of the parabola as constants or coefficients?
A) Y – 15 = X2 – 6X
B) Y = X(X-8) + 15
C) Y+1 = (X-4)^2
D) Y = (X-3)(X-5)
If you could use some help solving these or prepare for you SAT Math exam, you can schedule a one-on-one session with me anytime or contact me using the contact form above.
