3.4 SAT Math: Factoring Common Factors

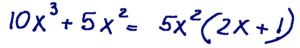
Factoring is an essential tool in algebra and for SAT math problem solving. It comes from the word “factor,” which means “An integer that divides into another integer exactly.” Like 2 divides into 8, also 4 divides into 8. So 2 and 4 are factors of 8, because 8 is divisible by them.

8 : 4 = 2

Also, 1 and 8 are factors of 8, since 8 is also divisible by 8 and 1.

8 : 8 = 1

Same is true when we switch the signs around, like -2 and -4 are also factors of 8, since 8 is divisible by them too.  And -1 and -8 are factors of 8, because 8 is divisible by -1 and -8.

With this in mind, we can also factor variables that are labeled with letters, such as X, Y, Z, etc.

Say, what are the factors of X⁶? They are X, X², X³, X⁴, X⁵, X⁶.  X⁶ can be divided by all of them, therefore they are called factors of X⁶.

What combinations of two factors of X⁶ can make a product of X⁶?

X² * X⁴ = X⁶ [Based on Exponent Rule: X^a * X^b = X^a+b and X^a / X^b = X^a-b]

Also, a combination of X³ and X³ factors make a product of X⁶.

X³ * X³ = X⁶

And so forth…

Let’s do an example. Factor the following:

10X³ + 5X²

We’re going to use a distributive property over multiplication to do factoring. We’re going to find the greatest common factor and move it outside of the parentheses.

First lets deal with the coefficients. What is the greatest common factor for 10 and 5?

Lets list all the factors for 10, they are 10, 1, 5 and 2.

Lets list all the factors for 5, they are 5 and 1.

So, what is the greatest common factor for 10 and 5?

The greatest common factor for 5 and 10 is 5. So this is the factor we are going to use.

Let’s factor out 5 now.

When we factor 5 out of 10, we are left with 2, since 10/5 = 2.

When we factor 5 out of 5, we are left with 1, since 5/5 = 1.

So now we can write our expression with 5 factored out of the coefficients using a distributive property:

5(2X³ + 1X²) or

5(X³ + X²)

Once we factored out the coefficients, we can move onto the variables, in this case it’s just an X.

What are the factors for X³ and X²?

Factors for X³ are X, X², X³ and 1.

Factors for X² are X, X² and 1.

What is the greatest common factor for X³ and X²?

The greatest common factor for X³ and X² is X². So this is the factor we are going to use.

Let’s factor out X².

When we factor X² out of X³, we are left with X¹ or simply X.

When we factor X² out of X², we are left with 1, since when you divide a number or a variable by itself, you’re left with 1. X²/X² = 1.

So now we can write our expression with X² factored out:

5X²(2X + 1)

Since we don’t have any more variables, we are done. If we had other variables, such as Y, Z or others, we would have to continue factoring each variable the same way we just did with the X. But in this case the answer is 5X²(2X + 1).

[To check your answer, just multiply 5X² by what’s in the parenthesis and you should get the same expression that you started out with.]

Practice Problems

Now you should continue practicing factoring. Please try to factor these expressions.  If you are still having problems, I will be happy to help you.  Book a session with me here.

32X⁴ + 8X²

45X⁷Y⁶ + 9X⁵Y³

60X⁵Y⁸Z³ – 15⁴5YZ⁵

SAT Math Example Problem

2X(2X+3) + 4(2X+3) = aX2 + bX + c

In the equation above, a, b and c are constants.  If the equation is true for all values of X, what is the value of b?

We need to change the left side of the equation into the expanded form, that would take the form of the equation on the right. When we do that, we’ll be able to identify coefficients a, b and c for this equation.

The left side of the equation has two addition terms 2X(2X+3) and 4(2X+3).

Both terms have one factor in common, which is (2X+3).

Let’s factor out (2X+3)

(2X+3) (2X+4) = aX2 + bX + c

Now we’re going to use distributive property of addition over multiplication.  Each term inside the first parentheses needs to be multiplied by each term inside of the second parenthesis.

2X*2X + 2X*4 + 3*2X + 3*4 =  aX2 + bX + c

Now let’s multiply

4X^{2 + 8X + 6X + 12 = aX2 + bX + c}

Now let’s add the like terms on the left side

4X^{2 + 14X + 12 = aX2 + bX + c}

Now our equation on the left side is in the same form as the equation on the right side.  We can now see that a=4, b=14 and c=12.

So the value of b is 14.