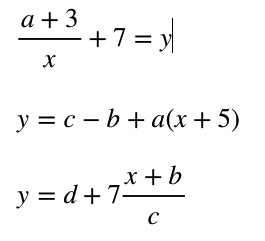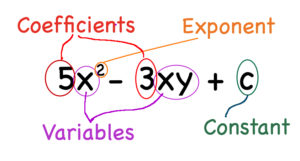
What Is An Algebraic Expression?
First off, the word “algebraic” comes from the word “algebra.” Algebra comes from Arabic word “al-jabr,” which means the reunion of broken parts. And “al-jabr” comes from Arabic “jabara”, which means reunite, restore. So “algebra” means the science of restoring what is missing and equating like with like.
When you are solving an algebraic expression you’re being asked to find a term of some sort, whether it’s a variable x or y, a constant, a coefficient, a power term, etc. So you are restoring what is missing by manipulating the expression, yet leaving it equal to the previous expression that you started out with.
Math is a language, where just like in any language certain rules exist. Listed below are the basic rules of algebra that you need to know in order to successfully manipulate an algebraic expression, so that you can solve it. You will not be successful in SAT Math if you don’t follow these basic rules for algebra.
Rules For Manipulating An Algebraic Expression
Commutative property of addition says that it doesn’t matter what order to add the terms in, the sum will always be the same.
a+b = b+a
3+4 = 4 +3
7 = 7
Commutative Property of multiplication says that it doesn’t matter what order to multiply the terms in, the product will always be the same.
a*b = b*a
3*4 = 4 *3
12 = 12
Associative property of addition says that you can add and not worry about where you put the parenthesis.
(a + b) + c = a + (b + c)
(3+2)+4 = 3+(2+4)
5+4 = 3+6
9 = 9
Associative property of multiplication says that you can multiply and not worry about where you put the parenthesis.
(a * b) * c = a * (b * c)
(3 * 2)*4 = 3*(2*4)
6*4 = 3*8
24 = 24
Distributive property of addition over multiplication says that you need to multiply a multiplication term that is outside of the parentheses by all the addition terms inside the parentheses.
a * (b+c) = a * b + a* c
2 * (3+4) = 2*3 + 2*4
2*7 = 6 + 8
14 = 14
The order of operations always goes in the following priority
- operation in the parenthesis
- multiplication and/or division
- addition and/or subtraction
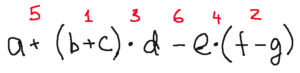
Let’s do an example:
1+(2+3)*4-5*(7-6)
First we need to do the operation in parenthesis (2+3) and (7-6), so we get
1+5*4-5*1
Next we multiply 5*4 and -5*1, so we get
1+20-5
Now we can do addition and the subtraction because they are in the order from left to right
1+20-5 = 16
The product of a number and its reciprocal is 1. The reciprocal of a number is 1 divided by the number.
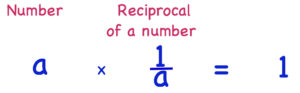
The additive inverse of a number is its negative.

The additive identity says that the sum of a number and its negative is 0.
3 + -3 = 0
The multiplicative identity says that if you multiply a number by 1, the product equals to the number itself.
a * 1 = 1 * a = a
3 * 1 = 1 * 3 = 3
Practice Problems
To practice the rules above try to do these on your own. Rewrite the expression in the form of x =